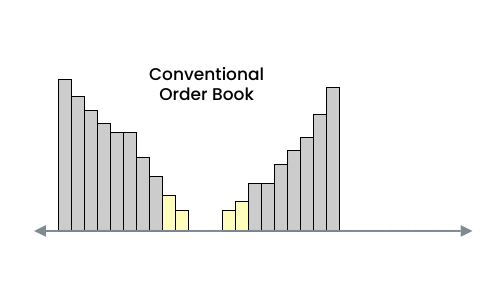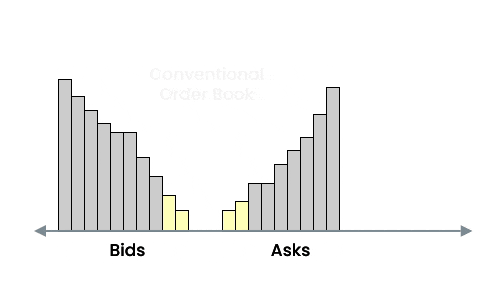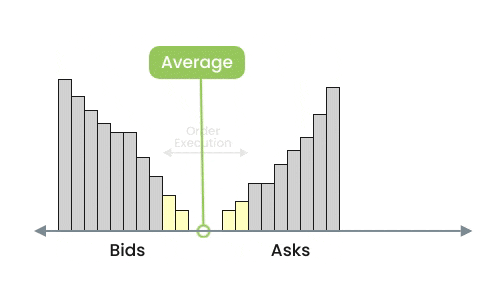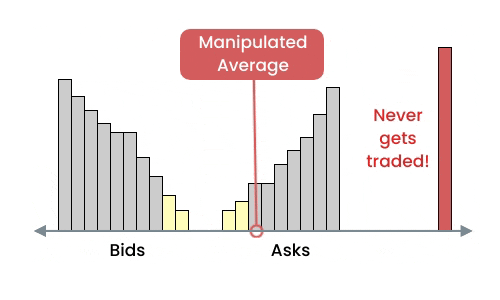
Well, you can. But a conventional order book is not usually "balanced" between bids and asks, and because large outside quotes on an order book are not price competitive they can be used to manipulate an average. In addition, because the order flow operates from the inside moving outward, the average tends to be more sensitive.
You could. However, order books can change frequently so you'd have to be prepared to incur the computational expense on every update. Alternatively, you could collect quotes over a limited time period and reward / slash quotes at the end of the period. That's not really real-time, however. In addition, the decision on the slashing cutoff point would be somewhat arbitrary.
Yes! Microtick already does this - and in addition, because prices can change rapidly, it lets each quote specify its own "standard deviation". In option pricing terminology this is known as the premium price based on volatility.
With Microtick each participant can select the time window they want to maintain a quote for - the longer the time window you choose the less frequently a quote needs to be updated.
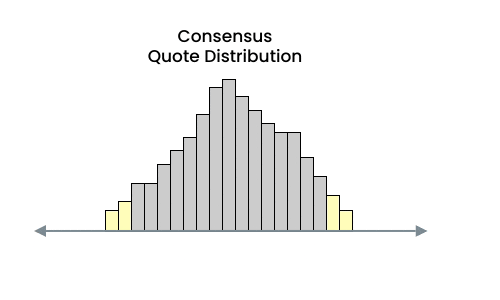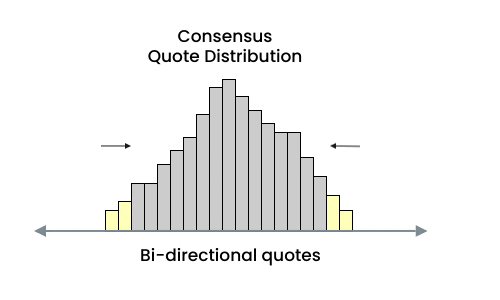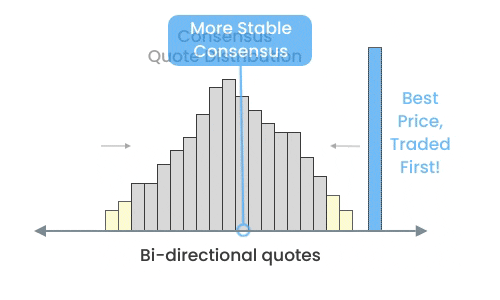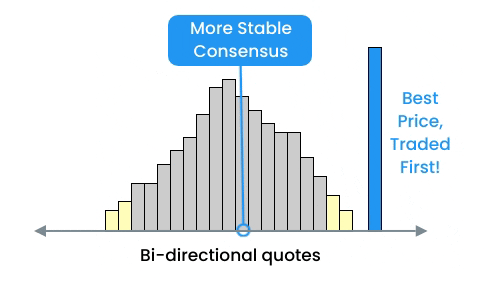
Because Microtick price discovery is based on a Shelling point price consensus and not competing bids / asks on the underlying asset, the quote distribution is inverted - with the most competitive quotes (in yellow) on the outside. Manipulative quotes are actually the most price competitive and will be traded from the market first. In addition, they can't be placed arbitrarily far away from the consensus due to pricing rules enforced by the smart contract.